Projectile Motion

Imagine throwing a ball to someone. As the ball travels horizontally through the air, it also travels vertically because of the effects of the force of gravity. Any object moving in this way is.

Projectile Motion with ExamplesArticle IndexPROJECTILE MOTIONWe see one dimensional motion in previous topics. Now, we will try to explain motion in two dimensions that is exactly called “projectile motion”. In this type of motion gravity is the only factor acting on our objects.

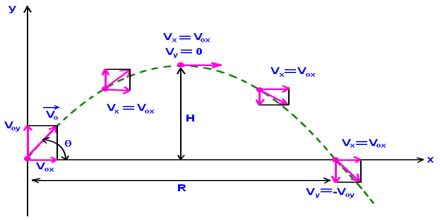
We can have different types of projectile type. For example, you throw the ball straight upward, or you kick a ball and give it a speed at an angle to the horizontal or you just drop things and make them free fall; all these are examples of projectile motion.In projectile motion, gravity is the only force acting on the object. I will explain this sentence with a picture and examples. First, look at the given picture which shows the motion path, velocities in different points and forces acting upon the object doing projectile motion.As you see in the picture given above, we have a projectile motion and velocity components at different positions. At the beginning the ball is thrown with an angle to the horizontal.

V is its velocity and its direction is northeast. Vx and Vy are the X and Y components of our velocity. If we look at the forces acting on our ball we see only the gravity as a force.

We examine our motion in two parts, first one is horizontal motion and second one is vertical motion. When we look at the horizontal motion of the object we see that it looks like example solved in free fall motion section. In vertical as you can see in the picture, our velocity is decreasing in the amount of gravitational acceleration. At the top where it reaches its maximum height vertical component of our velocity becomes zero as in the case of free fall examples. After Vy becomes zero our ball changes its direction and make free fall now. At the same levels magnitudes of Vy are the same however, their signs are opposite. Right side of our picture has “-“sign in front of the Vy because its direction is downward.

Finally, when the ball hits the ground Vy reaches its beginning magnitude but opposite in direction. We see the effect of gravity on vertical motion. Now, let’s look at the horizontal part of our projectile motion. This part is so easy that you can understand from the picture, our horizontal component of velocity is constant during the motion. Why it is constant? What changes the velocity?

In previous section we learned force concept that causes change in the state of motion. Look at our horizontal motion carefully. Is there any force acting on our object in horizontal direction +X or –X? The answer is actually no. However, in –Y direction gravity is acting on our object which makes Vy decrease and becomes zero at the top.

All these explanations say that, we have two motions in projectile motion. One of them is constant motion in horizontal and other one is free fall under the effect of gravity in vertical. We tried to explain projectile motion with words. Now it is time to give equations of motion under two titles.1. Vertical motion:In vertical we said that gravity acts on our objects and give it negative acceleration “-9,8m/s²”.

This means that, our velocity decreases -9,8m/s² in each second. We find the velocity of the free falling object by the equation V=g.t.

If we have initial velocity then, our equation becomes;V=Vit+gt where acceleration is -9,8m/s²The distance in free fall is calculated by the equation;As in the velocity case our distance is calculated considering the initial velocity of the object by the formula;We put “-“sign because direction of g is downward.2. Horizontal motion:We have constant motion in horizontal because there is no force acting on our object in horizontal direction. Thus, the X component of velocity is constant and acceleration in X direction is zero.

Milwaukkee shockwave impact duty driver bits are engineered to be most durable, best fitting driver bits on the market. The opitmized shockzone geometry is unique for each tip type to provide up to 30x more torque vs. Other impact bits.The precise fit coutom machined tip prervente stripping and reduce wobble while the custom alloy 76 steet and proprietary heat treat maximizes resistance to. Duty driver 3. Featuring Shockwave Impact is this Milwaukee Shockwave Impact Duty driver bits. It is engineered to be the best fitting driver bits on the market. Shockwave driver bits are built to deliver extreme durability for the most demanding applications. Our latest GeForce Game Ready driver delivers day-one optimizations and enhancements for Call of Duty Ⓡ: Warzone, a new free-to-play massive combat arena for up to 150 players with Call of Duty Ⓡ: Modern Warfare’s signature gameplay.

The equation that is used to calculate distance and velocity is given below.You can find distance traveled, time elapsed from this equation.Now I will solve some examples related to the each type of projectile motion.Example In the given picture below, Alice throws the ball to the +X direction with an initial velocity 10m/s. Time elapsed during the motion is 5s, calculate the height that object is thrown and Vy component of the velocity after it hits the ground.Example John kicks the ball and ball does projectile motion with an angle of 53º to horizontal. Its initial velocity is 10 m/s, find the maximum height it can reach, horizontal displacement and total time required for this motion.

(sin53º=0, 8 and cos53º=0, 6)Example In the given picture you see the motion path of cannonball. Find the maximum height it can reach, horizontal distance it covers and total time from the given information. (The angle between cannonball and horizontal is 53º and sin53º=0, 8 and cos53º=0, 6).

For our purposes, a 'projectile'is any object that is thrown, shot, or dropped. Usually the object ismoving straight up or straight down. An object is launchedat 19.6meters per second (m/s) from a 58.8 -metertall platform. The equation for the object's height sat time tseconds after launch is s ( t )= –4.9 t 2 + 19.6 t+ 58.8, wheres isin meters. When does the object strike the ground?What is the height (aboveground level) when the object smacks into the ground? Well, zero, obviously.So I'm looking for the time when the height is s= 0.

I'll set sequal to zero, and solve:0 = –4.9 t 2+ 19.6 t + 58.80 =t 2 – 4 t – 120 =( t – 6)( t + 2)Then t= 6 or t= –2. The second solutionis from two seconds before launch, which doesn't make sense in thiscontext. (It makes sense on the graph, because the line crosses thex -axisat –2,but negative time won't work in this word problem.) So ' t= –2 ' is an extraneoussolution, and I'll ignore it.The object strikesthe ground six seconds after launch.Note the construction ofthe height equation in the problem above. The initial launch height was58.8meters, and the constant term was ' 58.8 '.The initial velocity (launch speed) was 19.6m/s, and the coefficient on the linear term was ' 19.6 '.This is always true for these up/down projectile motion problems.

(Ifyou have an exercise with sideways motion, the equation will have a differentform, but they'll always giveyou that equation.)The initial velocity is the coefficient for the middle term, and the initialheight is the constant term. And theon the leading term comes from the force of gravity. This coefficientis negative, since gravity pulls downward, and the value will either be' 4.9 '(if your units are 'meters') or ' 16 '(if your units are 'feet'). In general, the format is:s ( t )= – gt 2+ v 0 t+ h 0.where ' g 'here is the ' 4.9 'or the ' 16 'derived from the value of the force of gravity (technically, it's halfof the force of gravity, but you probably don't need to know that rightnow), ' v 0 '('vee-naught', or 'vee-sub-zero') is the initial velocity,and ' h 0 '('aitch-naught', or 'aitch-sub-zero') is the initialheight.Memorize this equation(or at least its meaning), because you may need to know this on the test. An object in launcheddirectly upward at 64feet per second (ft/s) from a platform 80feet high.

What will be the object's maximum height? When will it attainthis height?Hmm. They didn't giveme the equation this time. But that's okay, because I can create theequation from the information that they didgive me. The initial height is 80feet above ground and the initial speed is 64ft/s. Since my units are 'feet', then the number for gravitywill be 16,and my equation is:s( t)= –16 t 2 + 64 t + 80They want me to find themaximum height.

For a negative quadratic like this, the maximum willbe at the vertex of the upside-down parabola. So they really want meto find the vertex. From,I know how to find the vertex; in this case, the vertex is at (2,144):h= – b / 2 a= –(64)/2(–16) = –64/–32 = 2k= s (2)= –16(2) 2+ 64(2) + 80 = –16(4) + 128 + 80 = 208 – 64 = 144But what does this vertextell me? According to my equation, I'm plugging in time values and extractingheight values, so the input ' 2 'must be the time and the output ' 144 'must be the height. Copyright© Elizabeth Stapel 2004-2011 All Rights ReservedIt takes two secondsto reach the maximum height of 144feet. An object is launchedfrom ground level directly upward at 39.2m/s. For how long is the object at or above a height of 34.3meters?My units this time are'meters', so the gravity number will be ' 4.9 '.Since the object started at ground level, the initial height was 0.Then my equation is:s( t)= –4.9 t 2 + 39.2 t.

AdvertisementSince this is a negativequadratic, the graph is an upside-down parabola. I can find the twotimes when the object is exactly 34.3meters high, and I know that the object will be above 34.3meters the whole time in between. Why 'two time', and howdo I know that the time period is between those two times?

Because thefirst time will be when the object passes a height of 34.3meters on its way up to its maximum height, and the second time whenbe when it passes 34.3meters as it is falling back down to the ground. So I have to solvethe following:–4.9 t 2+ 39.2 t= 34.3t 2– 8 t + 7 = 0( t– 7)( t – 1) = 0Then the object is at34.3 metersat one second after launch (going up) and againt at seven seconds afterlaunch (coming back down). Subtracting to find the difference, I findthat:The object is ator above 34.3 metersfor six seconds.Don't be surprised if manyof your exercises work out as 'neatly' as the above exampleshave. Many textbooks still engineer their exercises carefully, so thatyou can solve by factoring (that is, by quickly doing the algebra). However,heavy dependence on calculators is leading more texts to create 'interesting'(that is, needlessly complicated) exercises, so some (or all) of yourexercises may involve much more messy computations than have been displayedhere.

If so, study these 'neat' examples carefully, until youare quite sure you follow the reasoning. After the semesteris over, you discover that the math department has changed textbooks(again) so the bookstore won't buy back your nearly-new book.

You andyour friend Herman decide to get creative. You go to the roofof a twelve-story building and look over the edge to the reflectingpool 160 feetbelow. You drop your book over the edge at the same instant that Herman chuckshis book straight down at 48 feetper second. By how many seconds does his book beat yours into the water?Our initial launch heightswill be the same: we're both launching from 160 feetabove ground. And the gravity number, since we're working in feet, willbe 16.My initial velocity is zero, since I just dropped my book, but my buddyHerman's velocity is a negative 48,the negative coming from the fact that he chucked his book downrather than up. So our 'height' equations are:mine: s( t)= –16 t 2 + 160his: s( t)= –16 t 2 – 48 t + 160In each case, I need tofind the time for the books to reach a height of zero ('zero'being 'ground level'), so:mine: 0= –16 t 2 + 160, t 2 – 10 = 0,so t= ± sqrt(10)his: 0= –16 t 2 – 48 t + 160, t 2+ 3 t – 10 = 0, ( t + 5)( t – 2) = 0,so t= –5 or t= 2I will ignore the negativetime values.

His book hits the water after two seconds, and mine hitsafter sqrt(10) seconds,or after about 3.16seconds.